Mathématiques discrètes
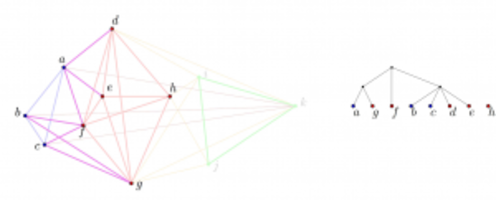
L’étude de systèmes complexes sur lesquels sont collectées des masses de données de plus en plus importantes nécessite la conception d’algorithmes de traitement optimisés, tirant avantage des spécificités des réseaux sur lesquels ils sont appliqués. L’étude de réseaux complexes montre que ces réseaux partagent souvent de mêmes propriétés structurelles : faible densité, distribution des degrés fortement asymétrique et propriété de « petit-monde ». Un enjeu est de comprendre si ces propriétés sont exploitables de manière algorithmique. L’étude des réseaux complexes ne se heurte pas seulement au problème de la taille et de la masse des données traitées, mais également à celui de leur évolution dans le temps. Comment les graphes réels évoluent-ils au fil du temps ?
Mathématique des graphes épars
Dans ce contexte général, les travaux menés au CAMS concernent l’analyse mathématique des graphes épars, c’est-à-dire des graphes ayant une faible densité locale d’arrêtes. Les outils mobilisés ici sont principalement ceux des mathématiques discrètes et de l’informatique théorique (complexité paramétrée, algorithmique distribuée, bases de données, etc.).
Les résultats mathématiques sont obtenus dans la limite asymptotique des très grands graphes. Ils contribuent à la théorie des graphes et à des développements algorithmiques. En collaboration avec le mathématicien Jaroslav Nešetřil (Prague), le CAMS a développé une théorie structurelle des graphes épars. Cette théorie a notamment permis d’identifier des classes de graphes pour lesquelles on démontre l’existence d’algorithmes efficaces adaptés à un large spectre de problèmes lorsqu’ils sont mis en œuvre sur des graphes de ces classes.
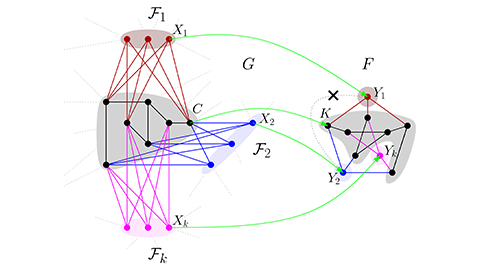
Les travaux menés au CAMS concernent également les réseaux possédant une structure sous-jacente de faible complexité, alors qu’ils semblent denses. Révéler ces structures latentes est analogue à la réduction de dimension effectuée en analyse de données par des méthodes d’apprentissage machine. Ce point de vue a conduit à une notion fructueuse de classes structurellement éparses.
Ce volet de mathématique fondamentale sur les graphes représente un thème historique de la recherche au CAMS (voir l’historique du CAMS). Il est aujourd’hui complété par des analyses et développements algorithmiques sur des réseaux complexes particuliers (échanges sur Twitter par exemple), relevant de la thématique Systèmes complexes du CAMS.
Principaux chercheurs impliqués
- Patrice Ossona de Mendez, Chargé de recherche au CNRS